Ising Model Simulations | Ashley S. Dale

Spin crossover systems have been successfully described[1] using an Ising-like Hamiltonian of the form

$$H = -J \sum_{\langle N \rangle}\sigma_i \sigma_j + \mu \sum_{i} \sigma_i$$

where $-J$ represents the interaction strength between the $i$th and $j$th site, $N$ represents the total number of sites, and $\mu$ represents the mean field. When combined with the Metropolis Hastings algorithm [2], simulations of how the system evolves can reveal some fun behaviors.

We can represent the mean field of the bistable spin crossover molecule as

$$\mu = \frac{\Delta}{2} - \frac{k_B T}{2} ln(g)$$

where $\Delta$ is the energy gap between the high-spin and low-spin state of the molecule, $T$ is the thermodynamic temperature of the system, and $ln(g)$ is the degeneracy ratio between the high-spin and low-spin states.

Here, a 3D lattice was simulated using fixed, non-interacting boundary conditions on the top and bottom of the cell, and periodic boundary conditions along the remaining dimensions. This represents a spin crossover thin film, where the top and bottom of thin film interface has pinned sites which are unable to update.

Simulation of 3D Ising Lattice. The top and bottom of the simulation cell have non-interacting sites, with the periodic boundary conditions along the remaining edges. Results presented at 2021 APS April meeting [3].

The compact minority-state domain is observed to persist and permeate the simulation cell due to the nearest-neighbors interaction[3]. This agrees with the minority compact state domains observed in XPS data for a spin crossover molecule [4]

The effect of the non-interacting sites can be probed by introducing a simulation where the non-interacting sites are replaced with sites that have a fixed value and are not free to update.

Adjusting the interactions of pinned sites. Presented at 2021 APS April meeting [3].

Repeating the simulation, we can see what happens when the fixed value sites take a value of $J=1$ (only $J=-1$ sites are shown)

Simulation of 3D Ising Lattice with pinned layers.

and when the fixed value sites take a value of $J=-1$ (only $J=1$ sites are shown)

Plotting this as a phase-transition diagram with the order paramter

$$n_{HS} = \frac{1 + \hat{\sigma}}{2}$$

we can see that the transition point from low-spin dominated to high-spin dominated state occurs at a different temperature depending on whether pinned sites are pinned to $J=1$ “FE pinned up”, pinned to $J=-1$ “FE pinned down”, or non interacting. The change in temperature indicates a different value for the energy gap $\Delta$.

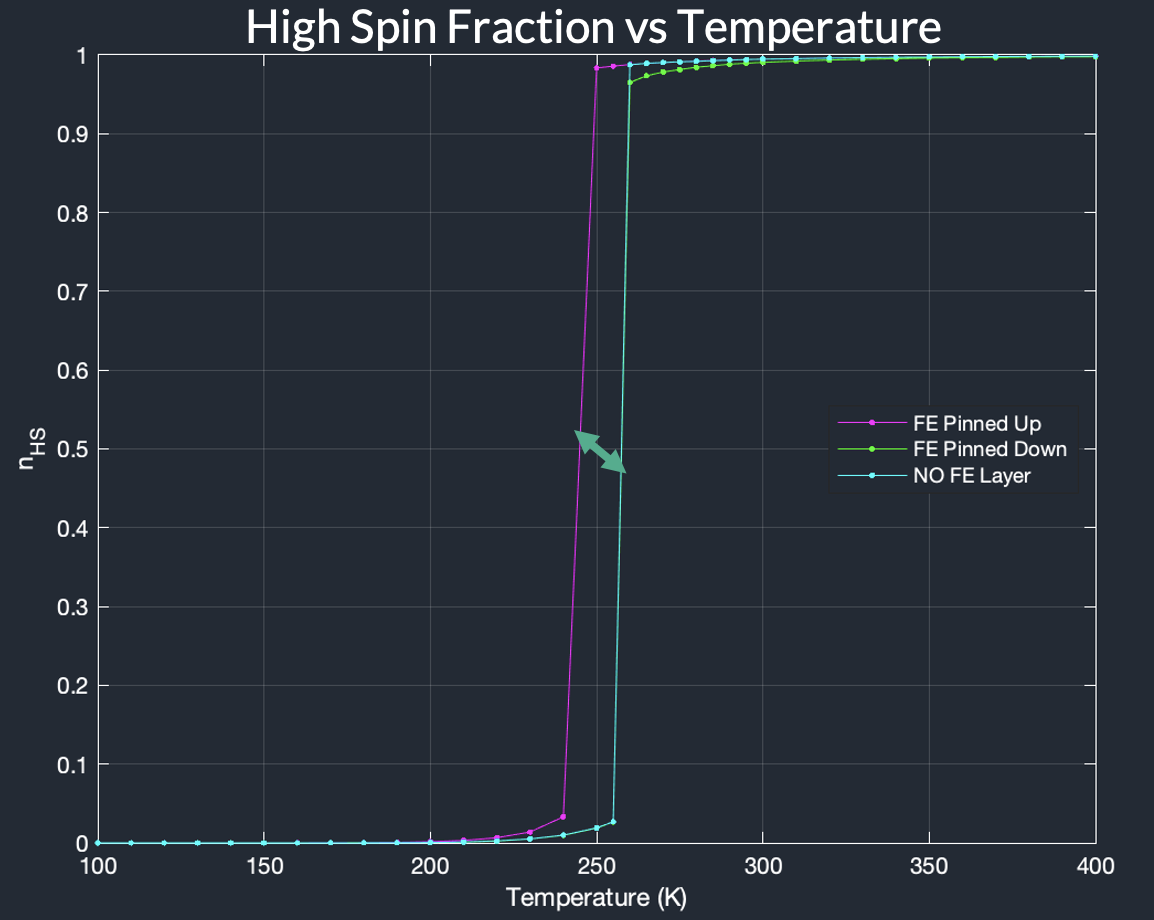
In a practical sense, this kind of pinning can be engineered into the system using different fabrication methods, or through heterostructure design[5].

[1]Two-dimensional Ising-like model with specific edge effects for spin-crossover nanoparticles: A Monte Carlo study

[2]Wikipedia: Metropolis Hastings Algorithm

[3]Determination of High-Spin to Low-Spin Phase Transition of Organic Spintronic Device by Monte Carlo Simulation of 3D Ising-like Model

[4]Intermolecular interaction and cooperativity in an Fe(II) spin crossover molecular thin film system

[5]Quantitative Study of the Energy Changes in Voltage-Controlled Spin Crossover Molecular Thin Films