Introduction

Power grid fault detection can be framed as an anomaly detection problem, and approached using machine learning techniques. In this notebook, voltage and current time series data from a three-phase power system is analyzed using a Long Short Term Memory Autoencoder (LSTM-AE). The LSTM-AE learns to take an input sequence and reconstruct; the reconstruction error is minimized during this process. When the LSTM-AE is required to reconstruct data outside the training data distribution, reconstruction error increases and signals that the data can be considered anomalous. Here, the LSTM-AE is trained using data from the power grid in a correct state, and the reconstruction scores of the network in various anomalous states are examined. The results are not promising. Anomalous scores are not strongly correlated with the onset of a power grid fault. This is attributed to the simplicity of the LSTM-AE architecture and lack of data. A brief discussion on what can be done to improve results is presented.

import numpy as np
import sklearn as skl
import pandas as pd
import csv
import matplotlib.pyplot as plt
import keras
from keras import layers

from tqdm import tqdm, trange
import tensorflow as tf
from scipy.signal import find_peaks

Data

The data may be downloaded directly from here and placed in the correct location.

From the original data authors:

We have modeled a power system in MATLAB to simulate fault analysis. The power system consists of 4 generators of 11 × 10^3 V, each pair located at each end of the transmission line. Transformers are present in between to simulate and study the various faults at the midpoint of the transmission line.

train_file = "data/classData.csv"
train = pd.read_csv(train_file)
test_file = "data/detect_dataset.csv"
test = pd.read_csv(test_file)

Train Data

Inspecting the train data to understand the available features:

train

	G	C	B	A	Ia	Ib	Ic	Va	Vb	Vc
0	1	0	0	1	-151.291812	-9.677452	85.800162	0.400750	-0.132935	-0.267815
1	1	0	0	1	-336.186183	-76.283262	18.328897	0.312732	-0.123633	-0.189099
2	1	0	0	1	-502.891583	-174.648023	-80.924663	0.265728	-0.114301	-0.151428
3	1	0	0	1	-593.941905	-217.703359	-124.891924	0.235511	-0.104940	-0.130570
4	1	0	0	1	-643.663617	-224.159427	-132.282815	0.209537	-0.095554	-0.113983
...	...	...	...	...	...	...	...	...	...	...
7856	0	0	0	0	-66.237921	38.457041	24.912239	0.094421	-0.552019	0.457598
7857	0	0	0	0	-65.849493	37.465454	25.515675	0.103778	-0.555186	0.451407
7858	0	0	0	0	-65.446698	36.472055	26.106554	0.113107	-0.558211	0.445104
7859	0	0	0	0	-65.029633	35.477088	26.684731	0.122404	-0.561094	0.438690
7860	0	0	0	0	-64.598401	34.480799	27.250065	0.131669	-0.563835	0.432166

7861 rows × 10 columns

Plotting the current data…

plt.figure(figsize = (10,4))
plt.scatter(np.linspace(0, len(train["Ia"]), len(train["Ia"])), train["Ia"], s=0.5, label="$I_a$")
plt.scatter(np.linspace(0, len(train["Ia"]), len(train["Ib"])), train["Ib"], s=0.5, label="$I_b$")
plt.scatter(np.linspace(0, len(train["Ia"]), len(train["Ic"])), train["Ic"], s=0.5, label="$I_c$")
plt.legend()
plt.xlabel('Time Step $\Delta t$')
plt.ylabel('Current $I$')
plt.savefig("figures/train_data_current.png")
plt.show()

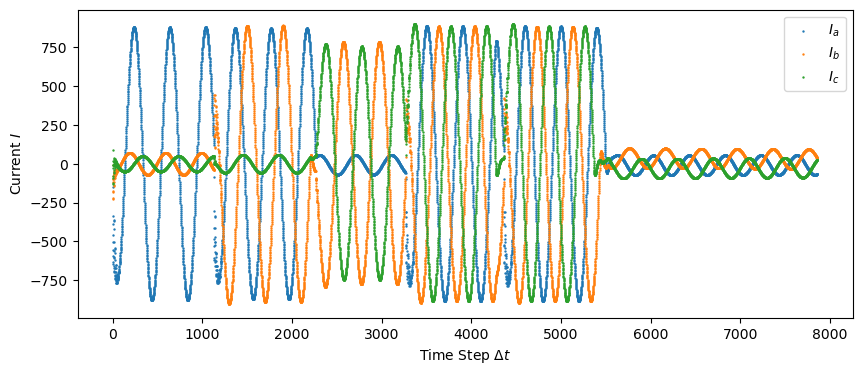
and the voltage data …

plt.figure(figsize = (10,4))
plt.scatter(np.linspace(0, len(train["Va"]), len(train["Va"])), train["Va"], s=0.5, label="$V_a$")
plt.scatter(np.linspace(0, len(train["Vb"]), len(train["Vb"])), train["Vb"], s=0.5, label="$V_b$")
plt.scatter(np.linspace(0, len(train["Vc"]), len(train["Vc"])), train["Vc"], s=0.5, label="$V_c$")
plt.xlabel('Time Step $\Delta t$')
plt.ylabel('Voltage $V$')
plt.savefig("figures/train_data_voltage.png")
plt.legend()
plt.show()

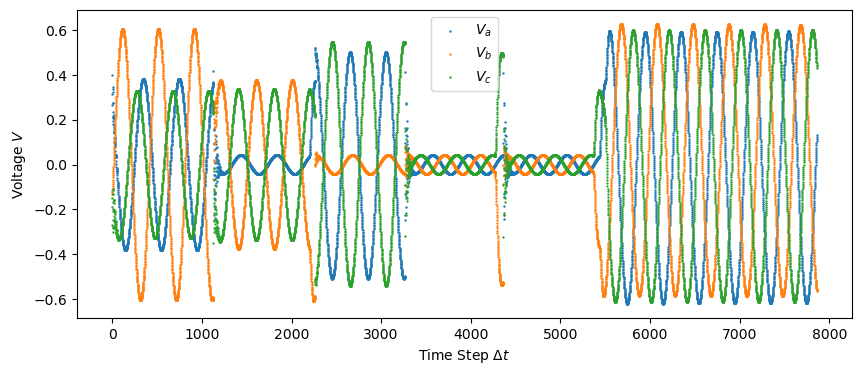
Convert one-hot labels to integers

One-hot	Description	Integer
[0 0 0 0]	No Fault	0
[1 0 0 1]	LG fault (Between Phase A and Ground)	9
[0 0 1 1]	LL fault (Between Phase A and Phase B)	3
[1 0 1 1]	LLG Fault (Between Phases A,B and Ground)	11
[0 1 1 1]	LLL Fault (Between all three phases)	7
[1 1 1 1]	LLLG fault (Three phase symmetrical fault)	15

train_arr = np.array(train)
num_rows = train_arr.shape[0]

new_labels = []
for idx in trange(num_rows):
    data_pt = train_arr[idx, :]
    label = str(int(data_pt[0]))+str(int(data_pt[1]))+str(int(data_pt[2]))+str(int(data_pt[3]))
    x = int(label, 2)
    new_labels.append(x)

100%|█████████████████████████████████████████████████████████████████████████████████████| 7861/7861 [00:00<00:00, 393500.70it/s]

training_data_idx = np.where(np.array(new_labels) == 0)

train_data = train_arr[np.array(new_labels) == 0][:, 4:]
y_labels = np.zeros(len(train_data))

not_train_data = train_arr[np.array(new_labels) != 0][:, 4:]

train['label'] = new_labels

No-Fault Data

plt.figure(figsize = (10,4))
plt.scatter(np.linspace(0, len(train_data), len(train_data)), train_data[:, 0], s=0.5, label="$I_a$")
plt.scatter(np.linspace(0, len(train_data), len(train_data)), train_data[:, 1], s=0.5, label="$I_b$")
plt.scatter(np.linspace(0, len(train_data), len(train_data)), train_data[:, 2], s=0.5, label="$I_c$")
plt.legend()
plt.xlabel('Time Step $\Delta t$')
plt.ylabel('Current $I$')
plt.savefig("figures/train_data_current.png")
plt.show()

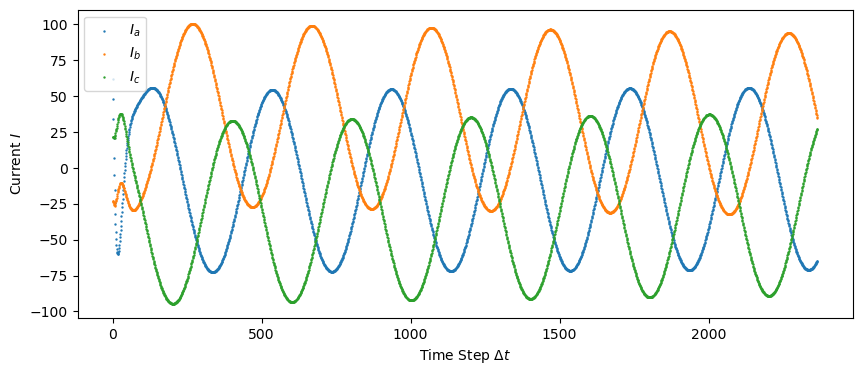
plt.figure(figsize = (10,4))
plt.scatter(np.linspace(0, len(train_data), len(train_data)), train_data[:, 3], s=0.5, label="$V_a$")
plt.scatter(np.linspace(0, len(train_data), len(train_data)), train_data[:, 4], s=0.5, label="$V_b$")
plt.scatter(np.linspace(0, len(train_data), len(train_data)), train_data[:, 5], s=0.5, label="$V_c$")
plt.legend()
plt.xlabel('Time Step $\Delta t$')
plt.ylabel('Voltage $V$')
plt.savefig("figures/train_data_voltage.png")
plt.legend()
plt.show()

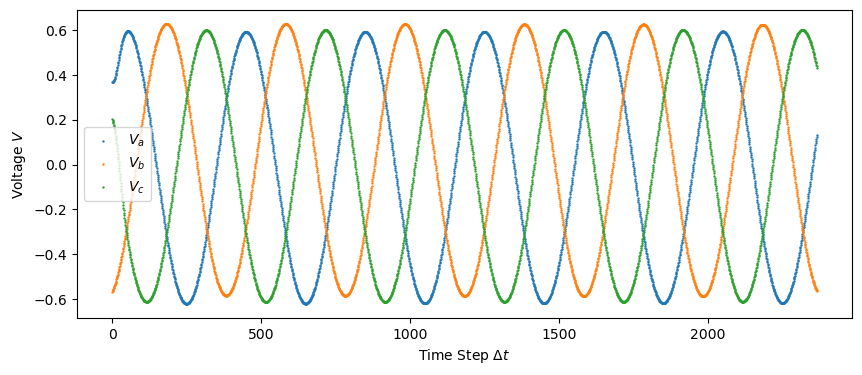
Format the data to be suitable for an LSTM-AE:

def make_seq(data_arr, window):
    data = []
    for idx in trange(len(data_arr) - window):
        data.append(data_arr[idx:idx+window, :])
    
    print(np.array(data).shape)
    return np.array(data)

timesteps = 55
crop_pts = np.mod(len(train_data), timesteps)

train_arr_noFault = make_seq(train_data, timesteps)

100%|████████████████████████████████████████████████████████████████████████████████████| 2310/2310 [00:00<00:00, 1426088.05it/s]

(2310, 55, 6)

Test Data

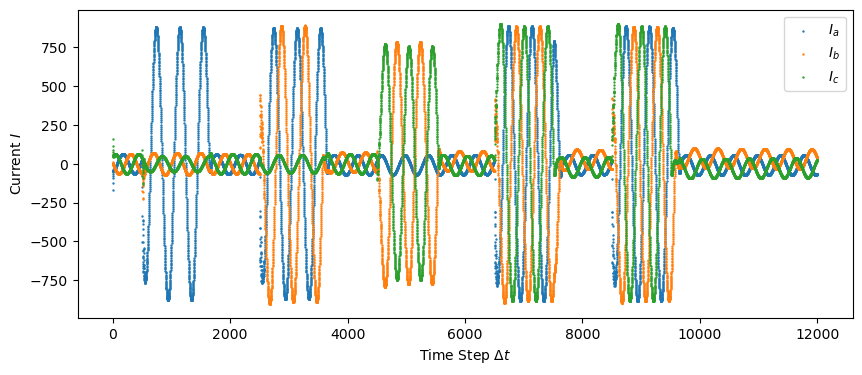
Inspecting and visualizing the test data…

test

	Output (S)	Ia	Ib	Ic	Va	Vb	Vc	Unnamed: 7	Unnamed: 8
0	0	-170.472196	9.219613	161.252583	0.054490	-0.659921	0.605431	NaN	NaN
1	0	-122.235754	6.168667	116.067087	0.102000	-0.628612	0.526202	NaN	NaN
2	0	-90.161474	3.813632	86.347841	0.141026	-0.605277	0.464251	NaN	NaN
3	0	-79.904916	2.398803	77.506112	0.156272	-0.602235	0.445963	NaN	NaN
4	0	-63.885255	0.590667	63.294587	0.180451	-0.591501	0.411050	NaN	NaN
...	...	...	...	...	...	...	...	...	...
11996	0	-66.237921	38.457041	24.912239	0.094421	-0.552019	0.457598	NaN	NaN
11997	0	-65.849493	37.465454	25.515675	0.103778	-0.555186	0.451407	NaN	NaN
11998	0	-65.446698	36.472055	26.106554	0.113107	-0.558211	0.445104	NaN	NaN
11999	0	-65.029633	35.477088	26.684731	0.122404	-0.561094	0.438690	NaN	NaN
12000	0	-64.598401	34.480799	27.250065	0.131669	-0.563835	0.432166	NaN	NaN

12001 rows × 9 columns

plt.figure(figsize = (10,4))
plt.scatter(np.linspace(0, len(test["Ia"]), len(test["Ia"])), test["Ia"], s=0.5, label="$I_a$")
plt.scatter(np.linspace(0, len(test["Ia"]), len(test["Ib"])), test["Ib"], s=0.5, label="$I_b$")
plt.scatter(np.linspace(0, len(test["Ia"]), len(test["Ic"])), test["Ic"], s=0.5, label="$I_c$")
plt.legend()
plt.xlabel('Time Step $\Delta t$')
plt.ylabel('Current $I$')
plt.savefig("figures/test_data_current.png")
plt.show()

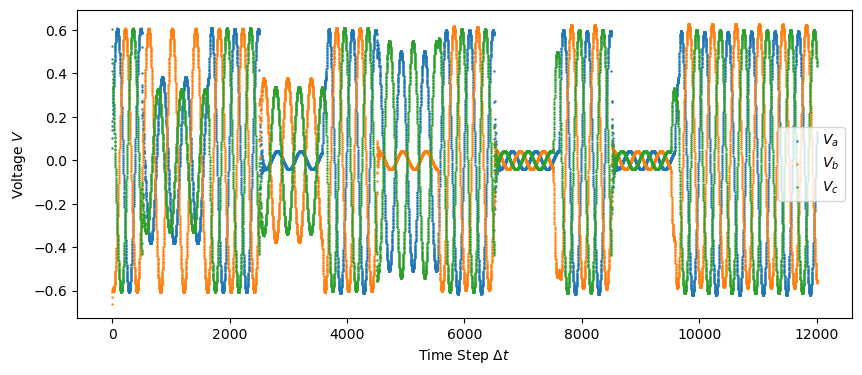
plt.figure(figsize = (10,4))
plt.scatter(np.linspace(0, len(test["Va"]), len(test["Va"])), test["Va"], s=0.5, label="$V_a$")
plt.scatter(np.linspace(0, len(test["Vb"]), len(test["Vb"])), test["Vb"], s=0.5, label="$V_b$")
plt.scatter(np.linspace(0, len(test["Vc"]), len(test["Vc"])), test["Vc"], s=0.5, label="$V_c$")
plt.legend()
plt.xlabel('Time Step $\Delta t$')
plt.ylabel('Voltage $V$')
plt.savefig("figures/test_data_voltage.png")
plt.show()

test_arr = np.array(test)[:, 1:7]
test_data = make_seq(test_arr, timesteps)

100%|██████████████████████████████████████████████████████████████████████████████████| 11946/11946 [00:00<00:00, 1486932.24it/s]

(11946, 55, 6)

train_full = np.array(train_arr)[:, 4:]
train_full_data = make_seq(train_full, timesteps)

100%|████████████████████████████████████████████████████████████████████████████████████| 7806/7806 [00:00<00:00, 1549050.77it/s]

(7806, 55, 6)

LSTM AE

Network Definition

input_dim = 6 
latent_dim = 4
epochs = 5000

inputs = keras.Input(shape=(timesteps, input_dim))
encoded = layers.LSTM(latent_dim,  activation="tanh")(inputs)

decoded = layers.RepeatVector(timesteps)(encoded)
decoded = layers.LSTM(input_dim, return_sequences=True)(decoded)
loss_fn = tf.keras.losses.MeanAbsolutePercentageError()

callback = tf.keras.callbacks.EarlyStopping(monitor='loss', patience=5, min_delta=0.00001)

model2 = keras.Model(inputs, decoded)
model2.compile(keras.optimizers.Adam(learning_rate=3e-5), loss_fn)
model2.summary()

Model: "model"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_1 (InputLayer)        [(None, 55, 6)]           0         
                                                                 
 lstm (LSTM)                 (None, 4)                 176       
                                                                 
 repeat_vector (RepeatVecto  (None, 55, 4)             0         
 r)                                                              
                                                                 
 lstm_1 (LSTM)               (None, 55, 6)             264       
                                                                 
=================================================================
Total params: 440 (1.72 KB)
Trainable params: 440 (1.72 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

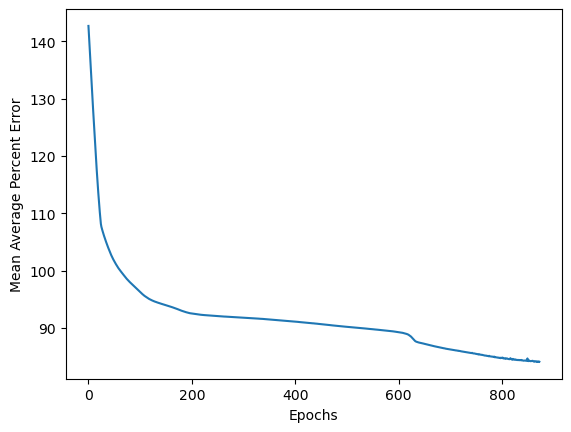
Training the model

history2 = model2.fit(train_arr_noFault, train_arr_noFault,
                epochs=epochs,
                batch_size=32,
                shuffle=True,
                validation_data=(train_arr_noFault, train_arr_noFault),
                      callbacks=[callback])

Epoch 1/5000
73/73 [==============================] - 5s 31ms/step - loss: 142.6676 - val_loss: 141.7920
...

Epoch 872/5000
73/73 [==============================] - 3s 47ms/step - loss: 84.1487 - val_loss: 84.0539

plt.plot(np.linspace(0, len(history2.history['loss']), len(history2.history['loss']), epochs), history2.history['loss'])
plt.xlabel("Epochs")
plt.ylabel("Mean Average Percent Error")
plt.savefig('figures/LSTM_loss.png')
plt.show()

Predictions

results = model2.predict(
    test_data,
    batch_size=32,
    verbose="auto",
    steps=None,
    callbacks=None,
    max_queue_size=10,
    workers=1,
    use_multiprocessing=False,
)

374/374 [==============================] - 4s 9ms/step

results2 = model2.predict(
    train_full_data,
    batch_size=32
)

244/244 [==============================] - 2s 10ms/step

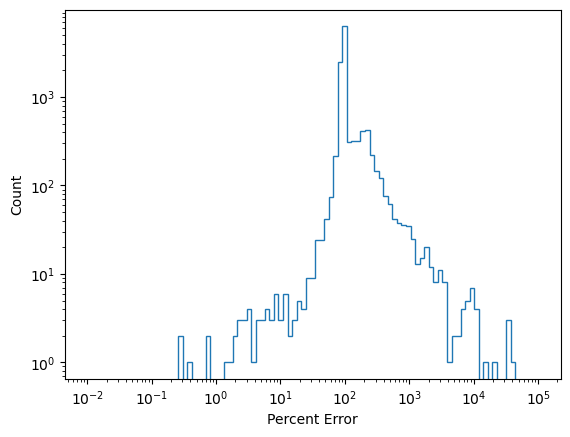
Calculate Statistics

err = []
for gt, recon in zip(test_data, results):
    err.append((np.sum([gt[0, :] - recon[0, :]]/gt[0, :])/6)*100)

err2 = []
for gt, recon in zip(train_full_data, results2):
    err2.append((np.sum([gt[0, :] - recon[0, :]]/gt[0, :])/6)*100)

counts, bins = np.histogram(np.abs(err), bins=np.logspace(-2, 5, 100))
fig, ax = plt.subplots(1, 1)
ax.stairs(counts, bins)
ax.set_yscale('log')
ax.set_xscale('log')
ax.set_xlabel('Percent Error')
ax.set_ylabel('Count')
plt.show()

Finding Anomalies

The error data can be treated as a time series, where the anomalies correlate with high error values. These values and the times can be identified using the find_peaks function.

peaks, heights = find_peaks(np.abs(err), height=1500)

fig, ax = plt.subplots(2, 1, figsize=(8, 4))
ax[0].scatter(peaks, heights['peak_heights'])
ax[0].plot(np.linspace(0, len(err), len(err)), np.abs(err), c='r')
ax[0].set_xticks([])
ax[0].set_ylabel('Reconstruction Error')
ax[1].set_ylabel('')
ax[1].scatter(np.linspace(0, len(test["Ia"]), len(test["Ia"])), test["Ia"]*100, s=0.5, label="$I_a$")
ax[1].scatter(np.linspace(0, len(test["Ib"]), len(test["Ib"])), test["Ib"]*100, s=0.5, label="$I_b$")
ax[1].scatter(np.linspace(0, len(test["Ic"]), len(test["Ic"])), test["Ic"]*100, s=0.5, label="$I_c$")
ax[1].set_xlabel('Time Step $\Delta t$')
ax[1].set_ylabel('Current $I$')
plt.tight_layout()
plt.show()

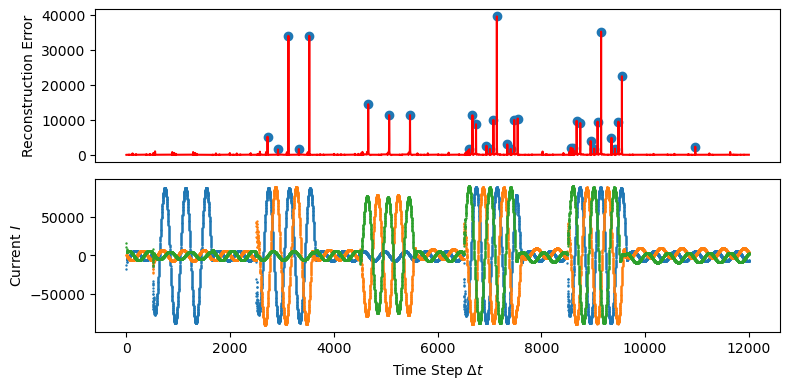
Ideally, the large red error peaks should be at the leading edge of each domain shift. This is not observed in the plot above. The blue dots on the Reconstruction Error plot shows which points have been identified as peaks.

fig, ax = plt.subplots(1, 1, figsize=(10, 4))

ax.plot(np.linspace(0, len(new_labels), len(new_labels)), np.array(new_labels)*100-1000, 'k', label='Fault Region')

ax.scatter(np.linspace(0, len(train["Ia"]), len(train["Ia"])), train["Ia"], s=0.25, label="$I_a$", alpha=0.5)
ax.scatter(np.linspace(0, len(train["Ib"]), len(train["Ib"])), train["Ib"], s=0.25, label="$I_b$", alpha=0.5)
ax.scatter(np.linspace(0, len(train["Ic"]), len(train["Ic"])), train["Ic"], s=0.25, label="$I_c$", alpha=0.5)
plt.legend()
ax2 = ax.twinx()
ax2.plot(np.linspace(0, len(err2), len(err2)), np.abs(err2), c='r', label='MAPE')
ax2.tick_params(axis='y', colors='red')

ax.set_xlabel('Time Step $\Delta t$')
ax.set_ylabel('Current I')
ax2.set_ylabel('MAPE')
ax2.spines['right'].set_color('red')
plt.tight_layout()

plt.savefig('figures/results2_I.png')
plt.show()

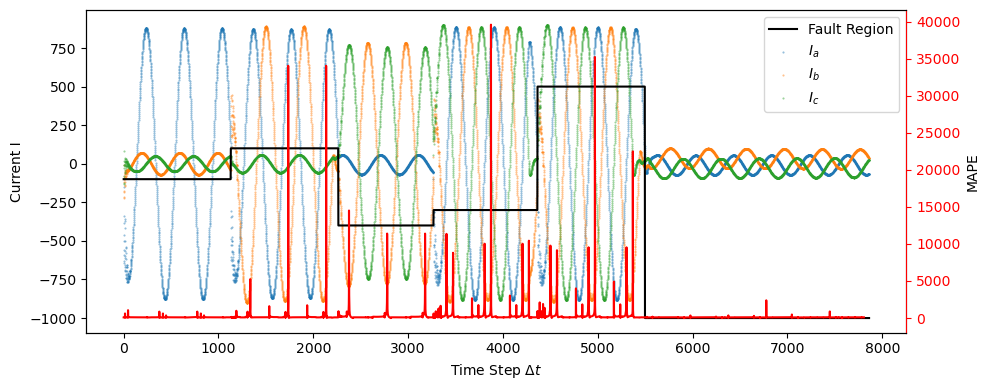
In the plot above, a black line indicating the original labeling has been superimposed with the error peaks to better show where the labeling and error anomalies coincide.

Summary

The LSTM-AE does generate anomaly scores for power grid fault conditions, the scores are not strongly correlated with the onset of a power grid fault and only weakly correlate with specific points in the phase of the power signal. However, in contrast to [1]–[4], the methods used here are excruciatingly simple. No data pre-processing, modified architectures, or additional information is used to identify anomalous points in the test data. The results show not only the challenges of machine learning for Smart Grid, but also its promise.

LSTM-AE Anomaly Detection